Fractales simples

Polígonos Fractales de n*n :


Cuadrados Fractales de n*n :


Sea  un fractal que comienza siendo un cuadrado, del que se suprime todo, dejando sólo 4 cuadrados en las esquinas de lado 1/4 cada uno y así sucesivamente en cada uno de los 4 cuadrados reducidos :

La dimensión de este cuadrado fractal "esquinado" será de log 4 / log 4 = 1; lo mismo que una línea recta. Las líneas del dibujo que unen los cuadrados de cada esquina deben ser borradas.

Conservemos ahora, para un cuadrado fractal de n*n -en el que cada  cuadrado puede contener n^2 cuadrados de lado 1/n cada uno- la primera y la última fila y la primera y última columna, quitando lo demás. Nos quedarán 2*n+2*(n-2) = 4*(n-1) cuadrados de lado 1/n  y la dimensión del cuadrado fractal construido así será de                 D = log(4*(n-1)) / log(n), que cuando n tiende a infinito toma el valor D = 1. Familia infinita de cuadrados fractales que para valores grandes de n, se acercan a la dimensión de una recta.

Para n=3  D = log 8 / log 3 = 1,89  :  La Alfombra de Sierpinski.
Para n=4  D = log 12 / log 4 = 1,79
Para n=5  D = log 16 / log 5 = 1,72

Para n=100 D = log 396 / log 100 = 1,30

Aquí va un cuadrado fractal de 4*4 .

Triángulos fractales de n*n :

Triángulos fractales equiláteros  de n*n (subdivididos en n^2 triángulos de lado 1/n cada uno) en  que se conservan los contornos  con los triángulos más pequeños y se quitan los del centro. Se necesitan 3*(n-1) de ellos para cubrir  los 3 lados. La dimensión es:
D= log (3*(n-1)) / log (n).     Cando n tiende a infinito D tiende a 1.



n = 2 D = log 3 / log 2 = 1,58 :  El Triángulo fractal de Sierpinski
n = 3 D = log 6 / log 3 = 1,63
n = 4 D = log 9 / log 4 = 1,58
n = 5 D = log 12 / log 5 = 1,54
n =100 D = log 297 / log 100 = 1,24



Aquí abajo va un triángulo fractal de 4*4 :

Nota :  Me acabo de dar cuenta al ver que la dimensión para n=4, es la misma que para n=2, que he redibujado el triángulo de Sierpinski creyendo que era otro. Ello se debe a que la ecuación     3*(n^2-1) = (3*(n-1))^2 tiene como única solución válida para el caso,           n = 2; mientras que para el caso anterior de los cuadrados fractales, la única solución entera a 4*(n^2-1) = (4*(n-1))^2 es n = 1; la otra es 5/3.

La solución a t*(n^2-1) = (t*(n-1))^2 (1) es n = 1 o bien n = t+1 / t-1 que sólo es entero  para t = 3, con solución n = 2 (t = número de lados del polígono).

La ecuación (1) sólo es válida para t=3 o t=4, triángulos equiláteros o cuadrados ; polígonos regulares de ángulos internos no superiores a 90 º . El hexágono, y los demás polígonos regulares de 5 lados o más, no puede ajustarse a una recta sin dejar huecos de tal manera que la dimensión de un hexágono fractal con reducción 1 / n  y maximización de la ocupación de su contorno lineal  y de su interior por los hexágonos reducidos es para valores impares de n :    (t=6 D = log (t*(n-1) / 2) /  log n) y en su interior, sin solapar con el perímetro, caben (3*n^2+1) / 4   hexágonos regulares de longitud  de lado 1 / n .

No gano yo  para sorpresas ni sustos matemáticos,  que soy precisamente un amateur -y un desclasado. Soy en esta vida  bastante despistado y no había comparado las dimensiones del hexágono y del triángulo equilátero fractales, que son idénticas, puesto que escribo este texto a medida que lo voy descubriendo, en tiempo realmente real y sin desfase. Pero en el hexágono el aprovechamiento del espacio interno es diferente y mejor para valores impares de n. Por lo que la coincidencia de dimensión de fractalidad para n = 2 y n = 4 , no puede darse.

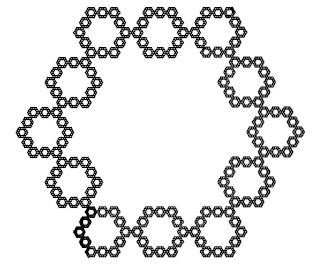
Primera iteración de un Hexágono Fractal de 5x5 en el que sólo se conservan los hexágonos adyacentes  al contorno del hexágono grande -la capa más externa-, es decir t*((n-1)/2) hexágonos pequeños con t = 6 y n =5 --> 12 hexágonos.

Tercera iteración del Hexágono Fractal de 5x5 .
 Yo hubiera preferido que los contornos originales de los hexágonos se vieran completamente, pero aún no sé cómo hacerlo con el programa  en java de Sistemas L. De idéntica dimensión D = log 12 / log 5 = 1,54 que un Triángulo Fractal de 5x5.

Tercera iteración de un Pentágono Fractal de 5x5 cuya dimensión es                                                    D = log (t*(n-1) / 2) / log n
Para t=5 y n=5      D = log 10 / log 5 = 1,43

Segunda iteración de Triángulo de 5x5

Segunda iteración de Triángulo de 3x3

Tercera iteración de Triángulo de 7x7

Tercera iteración de Cuadrado de 5x5

Cuarta iteración de Hexágono de 3x3.

 Se puede ver  como los centros de los hexágonos, en blanco, son  curvas fractales "copo de nieve" de Koch trianguladas equilateralmente. El fractal es complemento y frontera, en cada uno de los centros de sus hexágonos, de la curva de Koch. Es el hexágono fractal de Sierpinski de igual dimensión que el triángulo de 3x3: D = log 6 / log 3 = 1,63.

Segunda iteración de Hexágono fractal de 5x5 de 2 capas.

La capa externa compuesta de t*(n-1) / 2 (t=6, n=5) : 12 hexágonos y la segunda de 6. Un hexágono de      n x n  (n impar) tiene (n+1) / 2 capas concéntricas , desde el centro en que cabe 1 hexágono hasta la periferia en que caben múltiplos sucesivos de 6 : 1, 6, 12, 18, 24,...

En los triángulos de n x n, el número de capas concéntricas posibles es n / 3 si n =3*k (múltiplo de 3) y floor (n / 3) + 1 si  no es múltiplo de 3. La capa del centro será de 1 triángulo si n = 1 mod 3, de  4 triángulos si n = 2 mod 3 y de 9 triángulos si n = 0 mod 3 y n > 3.

En los cuadrados de n x n, el número de capas concéntricas posibles es n / 2 si n es par y  (n +1) / 2  si n es impar. La última capa será de 1 cuadrado si n es impar  o de 4 cuadrados si n es par.

Triángulo de 6x6 de 2 capas. La más externa de t*(n-1) = 3*5 = 15 triángulos (alternos en cada capa) y la otra de  6. La diferencia entre el número de triángulos alternos entre dos capas sucesivas es siempre de 9 salvo en el caso de n  = 1 mod 3 : (n = 4, 7, 10, 13, 16,..) en que entre las dos capas más céntricas hay una diferencia  en número, de 8 triángulos alternos, en vez de 9.
Dimensión : D = log 21 / log 6 = 1,70. En los casos en que , como en este, todas las capas son utilizadas por triángulos alternos equiláteros de lado 1 / n , la dimensión es de                                              D =  1+ log ((n+1)/2) /  log n.

Segunda iteración de triángulo de 10x10 con 2 capas. Sigo sin dominar ni entender bien el programa que utilizo para los dibujos y sigue no gustándome por su escasa indexación (si te equivocas codificando el dibujo, no tienes ningún medio de saber rápidamente donde. Y es en general difícil establecer recurrencias de tipo sencillo que permitan generalizar y sistematizar los dibujos. Por lo que este tipo de programación no es sencillo sino que es difícil y hasta árduo, de no estar acostumbrado). Las dos capas de segunda iteración en torno al interior del triángulo central no debieran estar pero no sé cómo quitarlas por ahora. Por otra parte las dos capas externas -aquí contiguas- pueden estar espaciadas y no tocarse, con una capa intermedia vacía -más estético y compensado a la vez . Para triángulos de 10x10 (n =10), el número de capas concéntricas es de floor(10 / 3) + 1 = 3 +1 = 4. Como 10 mod 3 = 1 (el resto de la división con resultado entero, de 10 por 3 , es 1), la capa más concéntrica, la cuarta, está formada por 1 único triángulo cuyo centro es también el del triángulo grande. ( "floor" de una división (atroz palabra colonial inglesa que evoca el suelo o la parte más baja de algo)  es su resultado entero descartando los decimales si los hubiera)

                                                   Hexágono de 7x7 con 3 capas; segunda iteración.


Nota:  Se establece un  Copyright en los dibujos,  y en el texto, que constituyan y sean novedad.